RECENT BLOG NEWS
Live Webinar: wolfSSL solutions for the AMD/Xilinx UltraScale+ MPSoC and Versal – Tailored for the Asia-Pacific Time Zone
Learn how to secure AMD/Xilinx UltraScale+ MPSoC Versal with wolfSSL’s high-performance cryptographic solutions.
As cybersecurity threats evolve, embedded systems require robust, high-performance cryptography. wolfSSL provides lightweight, high-speed, and FIPS 140-3 validated cryptography tailored for resource-constrained environments like AMD/Xilinx UltraScale+ MPSoC and Versal. With support for secure boot, firmware updates, and TLS 1.3, wolfSSL ensures end-to-end security while meeting key compliance standards such as DO-178 and CNSA 2.0.
Join wolfSSL Senior Software Engineer David Garske for a deep dive into best practices for securing AMD/Xilinx-based embedded systems. Learn how to implement secure boot, firmware updates, and TLS 1.3 while ensuring compliance and optimizing performance.
Register Now: wolfSSL solutions for the AMD/Xilinx UltraScale+ MPSoC and Versal – Tailored for the Asia-Pacific Time Zone
Date: June 11th | 7 PM PT / June 12th | 11 AM JST
(This webinar is tailored for the Asia-Pacific Time Zone)
What You’ll Learn:
- wolfSSL solutions for AMD/Xilinx UltraScale+ MPSoC and Versal
- Best practices for embedded security
- Post-Quantum Cryptography (PQC), CNSA 2.0, and Cyber Resilience Act (CRA) updates
- FIPS 140-3 and DO-178 compliance essentials
- Secure boot implementation and cryptographic performance
Register now to secure your AMD/Xilinx UltraScale+ systems with wolfSSL!
As always, our webinar will include Q&A throughout. If you have questions about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
Curve25519 Blinding Support Added in wolfSSL 5.8.0
As of wolfSSL version 5.8.0, support for Curve25519 blinding has been introduced. Although originally listed as a feature addition in the changelog, it is more accurately characterized as a mitigation for a potential side-channel vulnerability affecting specific builds. This feature offers optional hardening against power or electromagnetic (EM) analysis during Curve25519 private key operations. While such attacks are generally difficult to execute in practice, enabling blinding provides an additional layer of protection for devices that may be more susceptible to physical access or side-channel observation.
When Blinding Is Applicable
Blinding is only relevant for builds that use the C implementation of Curve25519 in wolfSSL. It is not available or necessary in the following cases:
- Assembly-optimized implementations (–enable-armasm / WOLFSSL_ARMASM, –enable-intelasm / USE_INTEL_SPEEDUP)
- The small footprint Curve25519 build (–enable-curve25519=small / CURVE25519_SMALL)
To enable blinding in the C implementation, define the macro WOLFSSL_CURVE25519_BLINDING. For example:
bash
CopyEdit
./configure --enable-curve25519 CPPFLAGS=-DWOLFSSL_CURVE25519_BLINDING
Affected APIs
Blinding hardens operations where the private key is used with scalar multiplication, such as:
- wc_curve25519_export_public_ex – when deriving the public key from a private key
- wc_curve25519_make_key – during key pair generation
- wc_curve25519_generic
- wc_curve25519_shared_secret_ex
If you are using the C implementation on hardware where physical side-channel exposure is a concern, it’s recommended to enable blinding and regenerate private keys used in these operations. Curve25519 blinding will be enabled by default for the C implementation in future wolfSSL releases.
Acknowledgments
Thanks to Arnaud Varillon, Laurent Sauvage, and Allan Delautre from Telecom Paris for reporting this.
If you have questions about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
wolfSSL Adds Support for Open Watcom Compiler
Introduction
The wolfSSL embedded SSL/TLS library has recently expanded its compatibility by adding support for the Open Watcom C/C++ compiler. This enhancement enables developers to build wolfSSL using Open Watcom across multiple platforms including Windows, Linux, and OS/2. This blog post explores the new Open Watcom support, its features, and how to leverage it in your projects.
What is Open Watcom?
Open Watcom is an open-source compiler suite derived from the commercial Watcom C/C++ compiler. It’s particularly valued for its:
- Cross-platform capabilities (Windows, OS/2, DOS, Linux)
- Efficient code generation
- Strong support for legacy systems
- Continued development by the open-source community
The compiler is especially important for maintaining and developing software for OS/2 and other legacy systems that still have active user communities.
New Features in wolfSSL for Open Watcom
The recent pull requests #8505 and #8484 have implemented several features to ensure wolfSSL works seamlessly with Open Watcom:
- Multi-Platform Support:
- Windows builds
- Linux builds
- OS/2 builds (particularly significant as OS/2 support is rare in modern libraries)
- Build Configuration Options:
- Single-threaded and multi-threaded builds
- Static library and DLL (Dynamic Link Library) options
- Compatibility with Open Watcom 1.9 and newer versions (2.0+)
- OS/2-Specific Enhancements:
- Socket handling for OS/2 networking
- Thread management for OS/2’s unique threading model
- Proper mutex implementation for OS/2
- Technical Improvements:
- Renamed OFFSETOF macro to WC_OFFSETOF to avoid conflicts with OS/2 headers
- Added proper time handling functions for Open Watcom
- Implemented conditional compilation for platform-specific code
- Fixed socket and I/O handling for cross-platform compatibility
Use Cases and Benefits
The addition of Open Watcom support opens up several possibilities:
- Legacy System Integration: Integrate modern TLS security into legacy systems running OS/2 or older Windows versions.
- Cross-Platform Development: Develop secure applications that can be compiled for multiple platforms using a single compiler.
- Educational Environments: Universities and educational institutions that use Open Watcom for teaching can now incorporate wolfSSL in their security curriculum.
- Embedded Systems: Some embedded systems with specific requirements may benefit from Open Watcom’s efficient code generation.
Summary
The addition of Open Watcom support to wolfSSL shows our versatility by supporting this compiler across Windows, Linux, and especially OS/2 platforms. This feature enables developers working with legacy systems, educational environments, and specific embedded platforms to leverage wolfSSL’s robust security features.
The implementation includes comprehensive support for different threading models and library types, ensuring that developers have flexibility in how they integrate wolfSSL into their projects. Whether you’re maintaining legacy applications, teaching security concepts, or developing cross-platform solutions, the Open Watcom support in wolfSSL provides a valuable tool in your development arsenal.
As the security landscape continues to evolve, this enhancement ensures that even systems using older or specialized compilers can maintain modern security standards through wolfSSL’s TLS implementation.
If you have questions about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
Meeting Secure Boot Compliance Requirements
In today’s regulatory environment, implementing a secure bootloader is no longer just a best practice – it’s becoming a compliance mandate. Recent cybersecurity regulations across the globe (from the EU to the US and beyond) explicitly call for measures like secure boot and firmware authenticity verification as requirements for connected devices. In this updated post (building on our earlier discussion of adding wolfBoot to legacy bootloaders), we highlight how upcoming frameworks make secure boot a must-have for compliance, and how wolfBoot’s features directly address these new regulatory requirements.
Table of Contents
- Introduction – Secure Boot as a Compliance Mandate
- EU Cyber Resilience Act: “Secure by Design” with Verified Boot
- U.S. Executive Order 14028 & Federal Initiatives
- UN R155 (Automotive): Cybersecurity and Boot Integrity
- Industrial Controls – IEC 62443 Requirements
- Medical Devices – FDA Cybersecurity Guidance
- Consumer IoT – ETSI EN 303 645 and Other Standards
- wolfBoot Capabilities Mapped to Compliance Needs
- Conclusion – Future-Proofing Legacy Systems
Introduction – Secure Boot as a Compliance Mandate
Just a few years ago, retrofitting a legacy system with a secure bootloader was mainly about proactive security. Now, it’s also about meeting regulations. Laws and standards are emerging which require devices to boot only authenticated firmware and maintain a trusted update process. For example, the EU Cyber Resilience Act (CRA) will mandate that connected products “implement secure boot processes verifying the integrity of software before execution”. Similarly, many U.S. initiatives (from Executive Order 14028 to federal IoT security guidelines) emphasize device integrity through measures like cryptographic signing and secure boot. In short, secure bootloader compliance is becoming essential.
Retrofitting your existing bootloader with a solution like wolfBoot can thus serve a dual purpose: elevating security and ensuring regulatory compliance. Below, we break down major cybersecurity frameworks across industries – each highlighting secure boot or firmware verification – and discuss how wolfBoot helps you conform to these firmware verification regulations.
EU Cyber Resilience Act: “Secure by Design” with Verified Boot
One of the most impactful new regulations is the European Union’s Cyber Resilience Act (CRA). The CRA is a broad law (expected to take effect in 2025–2026) that will require “products with digital elements” sold in the EU to meet stringent cybersecurity criteria. Crucially, secure boot is explicitly mentioned as part of being “secure by design.” The CRA mandates that manufacturers “implement secure boot processes verifying the integrity of software before execution.” This ensures that only trusted, untampered firmware runs on the device. In practice, devices must cryptographically authenticate their firmware at startup – exactly the capability that a secure bootloader like wolfBoot provides.
Other core tenets of the CRA include requiring secure software updates, vulnerability disclosure processes, and default secure configurations. Notably, the Act will enforce “secure by default” settings and the ability to apply updates/patches throughout a product’s lifecycle. Secure boot is the foundation for these measures – without a root of trust at boot, other protections can be bypassed. Manufacturers who fail to implement such controls risk non-compliance once the CRA is in effect.
How wolfBoot helps: wolfBoot was designed to ensure only authenticated firmware can run, aligning perfectly with the CRA’s secure boot requirement. On each boot, wolfBoot uses cryptographic signature verification to check the firmware’s integrity and authenticity before handing over execution. This means your device will “refuse to boot if the integrity checks fail,” as the guidelines demand. Additionally, wolfBoot’s built-in support for secure OTA firmware updates (with signing and version enforcement) satisfies the CRA’s calls for secure update mechanisms. By retrofitting wolfBoot into legacy devices, manufacturers can demonstrate compliance with EU CRA secure boot provisions without a complete redesign of their hardware.
U.S. Executive Order 14028 & Federal Initiatives
In the United States, while there isn’t a single omnibus law for IoT security yet, Executive Order 14028 (2021) – “Improving the Nation’s Cybersecurity” – has set the tone for higher security standards in software and devices. This Executive Order prompted federal agencies and critical infrastructure providers to adopt practices like zero-trust architecture and secure software development. One outcome has been the push for software supply chain integrity, where devices are expected to verify that only approved code runs on them. For example, federal IoT security guidelines (driven by the IoT Cybersecurity Improvement Act of 2020 and NIST recommendations) recommend secure boot functionality to ensure firmware integrity and authenticity. In other words, if you’re selling to U.S. government or critical sectors, features like secure boot and firmware signing are quickly becoming non-negotiable.
While EO 14028 itself focuses on government IT networks, it has cascading effects on IoT and embedded device requirements. The U.S. government is developing an IoT security labeling program (Cyber Trust Mark) and new FAR regulations for federal procurement, which are expected to include device integrity safeguards. Anticipating these, many U.S. device makers are now asking: “Where do we need secure boot, firmware signing, or mutual authentication?” as they navigate growing compliance complexity. In short, firmware verification regulations in the U.S. are largely policy-driven but converging on the same principle: untrusted code must be kept off devices.
How wolfBoot helps: By integrating wolfBoot, device manufacturers can proactively meet the emerging U.S. criteria for secure bootloader compliance. wolfBoot establishes a cryptographic chain of trust from reset vector onward – exactly the kind of defense that U.S. guidelines call for to counter supply chain attacks and firmware tampering. wolfBoot’s minimal footprint and FIPS 140-2 certified cryptography (via wolfCrypt) also ease the path for government use. Essentially, wolfBoot provides out-of-the-box firmware authenticity verification (digital signatures, hashing) that aligns with NIST’s core IoT baseline recommendations and the spirit of EO 14028. So if upcoming rules require attesting that your device “boots only trusted software,” wolfBoot gives you a clear affirmative.
UN R155 (Automotive): Cybersecurity and Boot Integrity
In the automotive world, cybersecurity requirements have been formalized in UNECE UN R155, a regulation that mandates a Cyber Security Management System for vehicle type approval (effective in EU, Japan, etc. from mid-2024). While UN R155 is process-oriented, it is accompanied by UN R156 (for Software Update Management) and heavily informed by the ISO/SAE 21434 standard. Together, these frameworks require automakers to ensure vehicles are protected from software tampering – which inherently includes ensuring only authenticated software can run on ECUs.
Specifically, UN R155 requires manufacturers to implement measures against unauthorized software changes and to verify software updates via cryptography. This means that every Electronic Control Unit in a car should reject code that isn’t properly signed or validated. Secure boot is a key part of meeting this requirement: by establishing a hardware-based root of trust and checking signatures at each stage of the boot chain, the vehicle can guarantee the integrity of its control software. Industry practice now views secure boot and runtime integrity as fundamental for automotive cybersecurity compliance. In fact, ISO 21434 (which UN R155 references) explicitly highlights “establishing trust anchors (Secure Boot) to ensure the integrity of initial boot software” as a best practice for protecting over-the-air updates and in-vehicle networks.
How wolfBoot helps: wolfBoot is well suited to automotive needs, where a verified boot chain and hardware trust integration are paramount. It supports leveraging a TPM 2.0 or HSM as the hardware root of trust, extending device identity into the boot process. For instance, wolfBoot can utilize a TPM’s secure key storage and PCR measurements to implement measured boot on automotive microcontrollers – aligning with UNECE’s expectations for “integrity of software throughout its operational lifecycle”. wolfBoot’s cryptographic verification at each boot stage and features like rollback protection directly address automotive threat scenarios. (UN R155 expects that if an attacker tries to downgrade firmware or inject malicious code, the system will detect it – wolfBoot enforces version checks and will refuse to load unauthorized or downgraded firmware.) Additionally, wolfBoot’s certifiability is a major plus in automotive: it’s designed with MISRA-C compliance in mind and can be delivered in a DO-178C certifiable format for aerospace/avionics use, indicating a rigor that automotive OEMs can leverage for ISO 21434 compliance. In short, retrofitting legacy ECUs with wolfBoot can help meet the stringent UN R155 secure boot expectations without waiting for the next vehicle generation.
Industrial Controls – IEC 62443 Requirements
Industrial and OT (Operational Technology) systems have their own cybersecurity standard: IEC 62443. Within this framework, IEC 62443-4-2 defines security capabilities for embedded devices used in industrial control systems. It explicitly calls for mechanisms to ensure the integrity of firmware and software, especially at boot time. One of the defined requirements is that “Embedded devices shall verify the integrity of the firmware, software, and configuration data needed for the component’s boot and runtime processes prior to use.” This essentially is a mandate for secure boot and secure firmware updates in the industrial context. Another related control in 62443 is to prevent the execution of unauthorized software on the device – again, a direct reference to having a whitelist of signed code.
For an operator of a power plant, factory, or critical infrastructure, this means that PLCs, RTUs, and controllers need cryptographic boot verification to achieve Security Level 2 or higher compliance. We see industry guidance urging use of secure boot in industrial gateways and PLCs as a way to meet 62443 malicious code protection requirements. In practical terms, if you’re upgrading or deploying industrial equipment, adhering to IEC 62443 likely means implementing a chain-of-trust from power-on reset through application launch.
How wolfBoot helps: wolfBoot’s core function – only allowing a trusted firmware image to run – directly satisfies the integrity verification requirement of IEC 62443-4-2. By integrating wolfBoot into a legacy PLC’s boot sequence, you equip it to “verify firmware integrity during boot and block execution if checks fail,” which is exactly what auditors will look for. wolfBoot’s support for a wide range of cryptographic algorithms (ECC, RSA, Ed25519, etc.) is important in industrial settings too, as it can match the algorithm policies of different organizations. Moreover, wolfBoot’s design is OS-agnostic and minimal, meaning it can run on bare-metal controllers with minimal overhead – a crucial factor for real-time industrial devices. It also offers features like dual-bank firmware updates with fail-safe rollback, which help maintain high availability (a failed update can automatically revert to the last known-good image). All these capabilities make it much easier to fulfill the IEC 62443 secure boot and update requirements on legacy industrial systems, bringing them up to par with modern security without a complete redesign.
Medical Devices – FDA Cybersecurity Guidance
Medical devices are another area where regulators are tightening requirements. The U.S. FDA in particular has issued guidance documents (most recently finalized in September 2023) that outline cybersecurity expectations for device makers. The FDA’s “Cybersecurity in Medical Devices: Quality System Considerations and Content of Premarket Submissions” guidance calls out the need for authenticity and integrity protections in devices. Manufacturers are expected to implement measures so that only trusted software can run on the device hardware. In fact, the FDA guidance explicitly recommends secure boot mechanisms: devices should “use secure boot mechanisms to ensure that only trusted and authenticated firmware/software is loaded and executed on the device”. It even says the device should validate the integrity of firmware during the boot process and refuse to boot if the check fails. This is a clear endorsement of secure boot as a baseline control for medical device cybersecurity.
Additionally, new U.S. legislation (the PATCH Act provisions in the 2023 omnibus) now requires that medical device premarket submissions include cybersecurity plans. This includes having the capability to “ensure secure and trusted updates and patches” throughout the device life. The FDA expects robust access control, logging, encryption of data, and secure update delivery, but all of those can be undermined if the device’s boot process is insecure. Hence, secure boot and a chain of trust (potentially anchored in hardware) are considered foundational to protect devices that could impact patient safety.
How wolfBoot helps: For medical device manufacturers updating legacy platforms, wolfBoot provides an immediate path to implement the FDA’s recommendations around boot integrity (“secure boot medical device” compliance). wolfBoot can be integrated into the device’s bootloader stage to perform cryptographic signature checks on the firmware image every time the device powers on. This ensures that any tampering (malicious or accidental) is detected and the device won’t run unverified code, addressing the exact use case described in FDA guidance. wolfBoot also supports encrypted firmware images, meaning even if a device’s update package is intercepted, an attacker cannot easily modify it in a way that would still pass signature checks. Another advantage is wolfBoot’s small footprint and minimal attack surface – it doesn’t rely on an OS or heavy runtime, which is ideal for constrained medical implants or devices where additional complexity itself can introduce vulnerabilities. By using wolfBoot’s secure boot and update features, a medical device maker can largely fulfill the FDA’s premarket cybersecurity expectations around software authenticity, and document that the device has a cryptographically verified boot chain from hardware up to the application.
Consumer IoT – ETSI EN 303 645 and Other Standards
For consumer IoT products (smart home, wearables, etc.), one key standard gaining worldwide adoption is ETSI EN 303 645. This European IoT security standard (which influences UK, Australia, and IoT labeling schemes) lays out baseline requirements for consumer devices. Among its provisions, ETSI 303 645 states that “The consumer IoT device should verify its software using secure boot mechanisms.”. It further notes that if an unauthorized change is detected, the device should alert the user and refrain from normal operation. This makes secure boot a recommended practice in the baseline, to ensure that even if malware somehow gets onto a device, it cannot persist after a reboot if it’s not properly signed. While ETSI 303 645 is phrased as “should” (best practice), regulators in the UK (through the Product Security and Telecommunications Infrastructure Act) and others are moving to make such provisions enforceable. In essence, consumer IoT devices are expected to have a mechanism to cryptographically validate firmware – including on initial boot and on updates.
Other industry-specific standards echo this theme. For example, ISO/SAE 21434 (automotive, as discussed) and even some IEEE/UL IoT standards emphasize secure boot. Globally, we see consensus in guidelines like NISTIR 8259 (U.S.) and the Global Semiconductor Alliance (GSA) IoT Security framework: devices must ensure code integrity. Manufacturers who implement secure boot are often able to meet multiple standards at once. As one IoT security report succinctly put it, “Secure boot and rollback protection [are] features [that] some regulations might require… to prevent malicious firmware installs or [firmware] manipulation”. This captures the idea that whether it’s a smart thermostat being certified for IoT security labeling or a new drone needing compliance, secure boot is a common requirement.
How wolfBoot helps: wolfBoot is highly portable and can be used even on small IoT SoCs, making it a practical choice to meet consumer IoT security requirements without heavy overhead. For instance, if you need to comply with ETSI 303 645’s secure boot recommendation, wolfBoot provides the functionality out-of-the-box: it will verify the firmware image’s signature at boot and can be configured to either halt or load a safe fallback image if verification fails. wolfBoot also supports anti-rollback via version numbers – which is a compliance advantage, ensuring that a device can’t be tricked into running an older, vulnerable firmware (this addresses the CRA’s “secure by default” rollback requirement and is generally good for any IoT standard calling for resilience). Additionally, because wolfBoot uses strong cryptography (and even offers post-quantum signature options), manufacturers can confidently claim adherence to “state-of-the-art” crypto practices as required by regulations. Whether it’s a smart camera needing to follow ETSI guidelines or a consumer router aligning to IoT Security Foundation recommendations, wolfBoot’s secure bootloader framework helps tick those compliance boxes. It essentially future-proofs legacy IoT products against the wave of new security standards.
wolfBoot Capabilities Mapped to Compliance Needs
Across all these domains – enterprise, automotive, industrial, medical, consumer – certain secure bootloader capabilities come up repeatedly as necessary for compliance. Here’s how wolfBoot addresses each of these critical requirements:
- Verified Boot Chain & Firmware Authentication: wolfBoot ensures that “only a trusted firmware image can run on the target device,” by using cryptographic signature verification on the firmware at every boot. This directly fulfills regulations demanding firmware integrity validation (CRA, IEC 62443, FDA, etc.). The chain-of-trust can start from a hardware root (e.g., a ROMed public key or TPM) and extends through wolfBoot to your application, providing end-to-end assurance.
- Cryptographic Signing (Modern Algorithms): wolfBoot leverages the wolfCrypt engine, supporting a wide range of algorithms for digital signatures – from ECDSA (secp256r1) and RSA-4096 to ed25519/ed448, and even post-quantum schemes like LMS/XMSS and ML-DSA. This means you can comply with whatever algorithm policies or certificate schemes your industry standard requires (e.g., FIPS-approved algorithms for government, or quantum-resistant keys for long-lived industrial devices). All firmware images are verified using these strong cryptographic checks on every update and boot.
- Anti-Rollback Protection: Many regulations (e.g., CRA and UN R156) require that devices cannot be rolled back to vulnerable firmware without authorization. wolfBoot implements version-based rollback protection – it will reject any firmware image with an older version number than what’s currently installed. This ensures attackers can’t slip a device back to an earlier insecure state. At the same time, wolfBoot offers controlled rollback in case of update failure: it keeps a backup of the last known-good firmware and can restore it if a newly updated firmware isn’t confirmed to be working. This gives the best of both worlds: security against malicious downgrade, and resilience for legitimate recovery.
- Secure Update Mechanisms (OTA support): Virtually all frameworks insist on secure firmware update processes. wolfBoot includes a highly reliable, transport-agnostic update mechanism. It supports firmware encryption in transit and at rest, and can work with various transports (UART, SPI, CAN, network, etc.) to retrieve updates securely. Whether your compliance need is to encrypt updates over-the-air or to use signed update bundles, wolfBoot has built-in tools to accomplish that. This directly maps to requirements in CRA, FDA guidance, and UN R156 that updates be delivered and applied in a secure manner.
- Hardware Root of Trust (TPM/HSM integration): Many regulations and standards favor or require using hardware security to anchor trust (e.g., TPM for secure boot is mentioned in automotive best practices). wolfBoot can integrate with hardware Secure Elements, TPM 2.0 chips, or MCU security features (Arm TrustZone-M, etc.). It supports using a TPM’s keys and PCR registers to validate the boot process, and can offload crypto operations to hardware accelerators. This means wolfBoot can meet certification requirements for a hardware-based root-of-trust, increasing assurance. For example, in an IIoT device you can store the wolfBoot verification public key in OTP or a TPM, and wolfBoot will use that to verify firmware – even if the main flash is compromised, the device won’t boot untrusted code.
- Minimal Attack Surface & High Assurance Implementation: wolfBoot is designed to be simple, compact, and safe. Its codebase is minimalist (focused purely on bootloading and crypto), which reduces potential vulnerabilities (crucial for meeting regulatory expectations of “secure by design”). It does not rely on an OS and has a tiny hardware abstraction layer. This lean design helps in formal certification and audit. In safety-critical industries, wolfBoot can be provided in a DO-178C level certifiable kit (for avionics), indicating the rigor of its development process. For industrial and automotive, its MISRA compliance and static analysis pedigree means it’s easier to validate against standards like ISO 26262 or IEC 61508 if needed. In short, wolfBoot can be described as a “certifiable” secure bootloader solution – as noted in our avionics partnerships, it’s a portable, certifiable bootloader and firmware update solution. This gives confidence when you need to show regulators evidence of software quality and trustworthiness.
By mapping wolfBoot’s features to the requirements set by these various cybersecurity frameworks, it’s clear that a lot of the heavy lifting for compliance is handled. Rather than writing a custom bootloader to meet each new standard, using wolfBoot allows you to leverage a proven secure bootloader that already aligns with best practices in multiple sectors.
Conclusion – Future-Proofing Embedded Systems
The writing is on the wall: secure boot and firmware verification are becoming mandatory across the board – from EU CRA secure boot requirements for consumer products, to automotive type approvals, to medical device approvals and more. What used to be considered a high-end security feature will soon be a baseline expectation under the law. For organizations with large installed bases of legacy devices, this could sound like a daunting challenge: do you need to scrap your existing bootloader or hardware to comply? Thankfully, the answer is no – with solutions like wolfBoot, you can retrofit secure bootloader compliance, even into your legacy systems relatively easily.
In our previous post, we demonstrated how wolfBoot can be used as a library or drop-in component to augment an existing bootloader with cryptographic verification (so you keep your custom update logic or hardware tweaks, but add the security layer). This approach of “retrofitting legacy bootloaders” is now not just about extending device life – it’s about ensuring those devices remain legal to use and sell in the coming years of stricter cybersecurity regulations. wolfBoot’s flexibility (OS-agnostic, multi-platform) means it can be applied to diverse legacy architectures, bringing them up to a compliance level roughly equivalent to a brand new design.
In summary, upcoming regulations are making secure boot not just a good security practice but a compliance checklist item. Implementing wolfBoot in your device can help you check that box with confidence. It provides the verified boot chain, robustness, and even documentation support (test evidence, etc.) to satisfy auditors and regulators. By choosing a trusted secure boot solution like wolfBoot now, you are future-proofing your legacy devices against evolving cybersecurity laws and protecting your customers from the risks of firmware attacks.
Compliance, security, and innovation can go hand-in-hand – retrofitting your legacy bootloaders with wolfBoot is a smart strategy to achieve all three. Feel free to reach out to the wolfSSL team to learn more about wolfBoot’s features (such as TPM integration, post-quantum signing, and safety certifications) and how they map to specific regulations in your industry. As always, we’re here to help ensure that your devices boot securely and comply with the latest cybersecurity requirements.
If you have questions about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
New Feature Spotlight: Offloading Extended Master Secret Generation to Hardware in wolfSSL
We’re thrilled to announce a new feature in wolfSSL 5.8.0: the ability to offload Extended Master Secret (EMS) generation to hardware, introduced in Pull Request #8303. Integrated into `–enable-pkcallbacks –enable-extended-master` builds, this enhancement empowers developers to leverage Trusted Execution Environments (TEEs) or custom hardware for EMS generation, boosting security and performance in TLS sessions. This makes wolfSSL an even more robust solution for embedded systems, IoT, and high-security applications.
What is Extended Master Secret Offloading?
The Extended Master Secret (EMS), defined in RFC 7627, strengthens TLS session security by tying the master secret to the full handshake transcript, mitigating man-in-the-middle attacks. The new feature in wolfSSL allows developers to offload EMS generation to hardware, such as a Trusted Execution Environment (e.g., ARM TrustZone, Intel SGX) or specialized cryptographic hardware. By using a custom callback function, you can delegate EMS computation to secure hardware, ensuring sensitive operations occur in a protected environment.
If you want to know more about using callbacks in wolfSSL or have questions about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
Live Webinar: Latest FIPS 140-3 developments at wolfSSL
Join us for an exclusive look into the Latest FIPS 140-3 Developments at wolfSSL, presented by Kaleb Himes, Senior Software Engineer at wolfSSL. This live webinar is scheduled for June 4th at 9 AM PT. Discover cutting-edge advancements in FIPS 140-3 compliance, Post-Quantum cryptography, and optimized solutions for Level 2 and Level 3 validation.
Register now: Latest FIPS 140-3 developments at wolfSSL
Date: June 4th | 9 AM PT
wolfSSL is FIPS 140-3 validated with 5-year Certification #4718. As the first to support Post-Quantum standards, wolfSSL delivers unmatched portability across dozens of hardware targets, establishing itself as a trusted leader in open-source cybersecurity.
This webinar will cover:
- Post-Quantum Full Submission: How wolfSSL is preparing for quantum-resistant encryption.
- FIPS 140-3 Level 2 & Level 3 Validation: Achieving rigorous standards with wolfSSL software and your hardware.
- Planned OE Additions: Get insight into our roadmap for expanding FIPS 140-3 certified OEs.
- Full Submission on Demand: Tailored modules, algorithm subsets, and boot loaders for embedded use-cases.
Register now to learn why industry leaders trust wolfSSL for their FIPS 140-3 projects and discover how you can stay ahead in cybersecurity!
As always, our webinar will include Q&A throughout. If you have questions about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
Expired Test Certificate: baltimore-cybertrust-root.pem and make check Failures
On May 12th, 2025, the test certificate baltimore-cybertrust-root.pem expired. This may cause issues with the test cases run during make check with wolfSSL builds that do not use the OpenSSL compatibility layer and have a filesystem enabled.
One of the unit tests attempts to load all Certificate Authorities (CAs) from the certs/external directory, which previously included this now-expired certificate. When this test is run with a wolfSSL configuration that will fail if any bad CAs are found among all CAs loaded, it will fail due to the certificate’s expiration.
This issue has been resolved in the wolfSSL master branch by the following pull request: https://github.com/wolfSSL/wolfssl/pull/8769
If you’re currently encountering failures during make check, we recommend removing the expired certificate from your local test environment by applying the changes from GitHub pull request 8769.
If you have questions about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
Firefox Gets FIPS 140-3 Power: wolfPKCS11 Unleashes wolfCrypt in NSS!
wolfSSL is thrilled to announce a significant milestone in browser security: the successful integration of wolfPKCS11 to provide FIPS 140-3 validated cryptography for the Mozilla Firefox browser. This is achieved by enabling wolfPKCS11 to serve as the backend cryptographic provider for Firefox’s Network Security Services (NSS) layer. This development represents a major step forward, bringing robust, federally-certified security to one of the world’s most popular web browsers.
This achievement builds directly upon a previously shared vision. Many may recall an earlier post, Why replace NSS with wolfSSL in Firefox?, which demonstrated the possibility of such an integration. It is with great excitement that this possibility is announced as a working reality. The core concept, replacing the underlying authentication implementations within NSS with the FIPS-validated capabilities of wolfCrypt via wolfPKCS11, has been brought to fruition.
For users and organizations operating in environments that require or prefer the assurances of FIPS 140-3 validated cryptography, this development is transformative. It means that Firefox can soon be leveraged with the formidable security backing of wolfSSL’s FIPS-certified cryptographic engine, wolfCrypt. While this advanced capability is fully functional and has been rigorously tested internally, it is important to note that it is not yet part of an official public release. Further announcements regarding public availability will be forthcoming. This progression from a proof-of-concept to a tangible, working solution underscores a commitment to not only innovate but also to deliver on complex technical challenges, reinforcing the reliability that is paramount in the security domain.
Why FIPS 140-3 in Your Browser is a Big Deal
Understanding the significance of this development begins with understanding FIPS 140-3. The Federal Information Processing Standard (FIPS) Publication 140-3 is a U.S. government standard developed by the National Institute of Standards and Technology (NIST). It specifies the security requirements for cryptographic modules, covering both hardware and software components that execute cryptographic functions. The primary role of FIPS 140-3 is to ensure that these cryptographic implementations meet stringent security benchmarks, thereby effectively protecting sensitive information. The gravity of this validation is starkly highlighted by NIST and the Canadian Centre for Cyber Security, which state that “non-validated cryptography is viewed as providing no protection to information—equivalent to plaintext”. This underscores the profound level of assurance that FIPS validation provides.
The mandate to use FIPS-validated cryptography is explicit for U.S. federal agencies when protecting sensitive information within their computer and telecommunication systems. This requirement frequently extends beyond direct government use, impacting contractors, organizations in regulated industries such as healthcare and finance, and entities pursuing critical certifications like the Cybersecurity Maturity Model Certification (CMMC). For other organizations, employing FIPS-validated cryptography serves as a clear indicator of a commitment to a high standard of security assurance.
Mozilla Firefox, along with other Mozilla products, relies on a set of libraries known as Network Security Services (NSS) for all its SSL/TLS, S/MIME, and other cryptographic operations. NSS is engineered to support cross-platform development and implements a comprehensive suite of internet security standards. A critical architectural feature of NSS is its utilization of the PKCS#11 standard. PKCS#11 is an API that governs communication with cryptographic tokens, which can be hardware accelerators, smart cards, or, as in this case, software-based modules often referred to as a “Software Security Device”. This adherence by NSS to the PKCS#11 standard is fundamental to the integration of wolfPKCS11. The combination of FIPS 140-3 defining what constitutes trusted cryptography and PKCS#11 providing how that trusted cryptography can be interfaced is powerful. Without NSS’s support for this standardized interface, replacing its cryptographic engine would be an extraordinarily complex, if not impossible, endeavor. This successful integration demonstrates how adherence to open standards can foster innovation and interoperability, ultimately benefiting end-users by making high-assurance cryptography accessible in mainstream applications like Firefox, potentially elevating the baseline for general web security expectations.
The wolfSSL Solution: wolfPKCS11 Powering NSS with FIPS-Certified wolfCrypt
The key to this enhanced security for Firefox is wolfPKCS11. This is wolfSSL’s robust implementation of the PKCS#11 API. The wolfPKCS11 module functions as an essential interface, or bridge, enabling applications that are designed to use the PKCS#11 standard (such as NSS) to access and utilize the comprehensive suite of cryptographic algorithms available within wolfSSL’s core cryptographic engine, wolfCrypt.
The integration leverages the “magic” of the PKCS#11 standard, which facilitates a “drop-in” replacement mechanism. NSS, by design, uses the PKCS#11 API to communicate with its default cryptographic library, which is softokn-freebl. The wolfPKCS11 module has been engineered to serve as a binary drop-in replacement for this default software security device. This means that, through modifications to configuration files rather than extensive code changes to Firefox itself, NSS can be directed to utilize wolfPKCS11. Consequently, all cryptographic calls from NSS are re-routed through wolfPKCS11 to the wolfCrypt engine. This elegant modularity, made possible by the PKCS#11 standard, significantly reduces the complexity and effort typically associated with integrating a new cryptographic provider into an established application like Firefox. The existence of this well-defined standard is a direct enabler of this relatively seamless integration path.
The true cryptographic power behind this solution resides in wolfCrypt, wolfSSL’s FIPS 140-3 validated cryptographic engine. wolfSSL has a distinguished history of achieving FIPS certifications, and wolfCrypt stands as a testament to this commitment, having attained FIPS 140-3 validation (the wolfCrypt module was one of the first in the world to receive a FIPS 140–3 Validation Certificate). It is this validation that imbues the Firefox integration with its robust security backbone and its capability to meet stringent compliance requirements. Beyond its FIPS validation, wolfCrypt is renowned for its exceptional performance, minimal footprint optimized for embedded systems, and extensive support for a wide array of cryptographic algorithms.
Seeing is Believing: FIPS-Powered Browsing (And Yes, It’s Real!)
It is understandable that FIPS-grade cryptography seamlessly operating within Firefox might sound almost too good to be true. To demonstrate that this is far more than just theoretical, it was even tested with some, shall we say, critical internet operations.
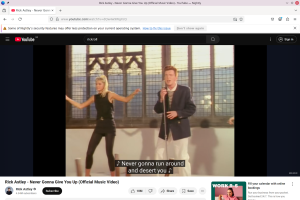
Caption: “Never Gonna Give Your Data Up: Firefox running with wolfSSL FIPS 140-3 security!”
Yes, that’s Firefox streaming a timeless classic. While the choice of content might be a playful rickroll, rest assured, the underlying FIPS 140-3 validated cryptography being provided by wolfPKCS11 and wolfCrypt is absolutely real and fully functional. If the system can handle real-world HTTPS traffic for streaming video (even this particular video), it is capable of many of today’s demanding browser use cases.
For those curious about how this appears “under the hood,” if one were to inspect Firefox’s security device manager, wolfPKCS11 would be visible as a loaded module.
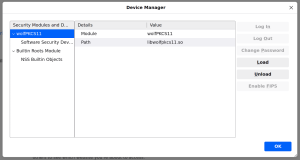
As mentioned, this powerful capability is confirmed and working seamlessly within our internal development environments. While it is not yet available in a public wolfPKCS11 release or as a standard component of Firefox distributions, work is progressing towards that goal. Keep an eye on the wolfSSL blog and official announcements for future updates.
Beyond the Browser: wolfSSL’s Commitment to Pervasive FIPS Security
The work to bring FIPS 140-3 validated cryptography to Firefox via NSS and wolfPKCS11 is not an isolated endeavor. It is a significant component of a much broader strategic initiative within wolfSSL: to make FIPS-certified cryptography readily and easily accessible across a diverse range of platforms and ecosystems.
This vision extends to enabling FIPS compliance across entire Linux distributions. There are ongoing efforts to integrate the wolfCrypt FIPS module with other critical system libraries, such as libgcrypt and GnuTLS. The ultimate objective is ambitious yet vital: “achieving FIPS 140-3 compliance across an entire Linux distribution”. Such an achievement would establish a unified, trusted cryptographic layer, thereby simplifying compliance efforts and significantly enhancing the security posture for countless applications and systems built upon these foundational open-source components. This strategy of embedding FIPS-validated technology deep within core operating system and application components positions wolfCrypt as a fundamental building block for secure systems, potentially establishing it as a de facto standard for FIPS cryptography in open-source environments.
Furthermore, the wolfPKCS11 module itself is designed with the future in mind. It is an evolving component, with enhancements such as upcoming support for the Leighton-Micali Signature (LMS) scheme planned. LMS is a stateful hash-based signature scheme, standardized in RFC 8554 and approved by NIST SP 800-208, notable for its quantum-resistant properties. This demonstrates a proactive stance towards emerging security threats. The engineering investment in wolfPKCS11 is therefore not limited to current FIPS standards; it is also paving a pathway towards post-quantum cryptography. This means that the very same integration mechanism being used to deliver FIPS 140-3 validated cryptography to Firefox today could potentially deliver post-quantum security in the future, thanks to the flexible and standards-compliant design of wolfPKCS11.
Conclusion: Secure Your Firefox Experience, Trust wolfSSL
To summarize this exciting development: wolfSSL has successfully made FIPS 140-3 validated cryptography a practical reality for the Firefox browser. This has been achieved by integrating the wolfPKCS11 module with Firefox’s Network Security Services (NSS), thereby allowing Firefox to leverage the proven strength of the wolfCrypt FIPS-certified engine.
The benefits of this integration are manifold. It provides access to high-assurance, FIPS-validated security within one of the world’s leading web browsers. For organizations with FIPS compliance mandates, it offers a significantly simplified path to meeting those requirements for browser-based activities. All of this is delivered with the robust, performant, and resource-efficient cryptography that wolfSSL is known for.
This advancement is another clear testament to wolfSSL’s leadership in embedded security, cryptography, and FIPS validation. The commitment at wolfSSL is to provide cutting-edge, reliable security solutions that meet the evolving challenges of the digital world. This successful integration reinforces that commitment and highlights the dedication to enhancing security for users everywhere.
Get in Touch / Download wolfSSL
Stay tuned to our blog for updates on the public availability of this feature!
If you have questions about any of the above, or how wolfSSL can help secure your applications, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
IronVelo Chooses wolfSSL for Secure Identity Solutions
In the realm of identity management, security is paramount. IronVelo, a company dedicated to building robust and reliable identity provider solutions, understands this critical need. To meet their stringent security requirements, IronVelo has partnered with wolfSSL, leveraging the power and reliability of the wolfCrypt cryptographic library. This collaboration highlights IronVelo’s commitment to security best practices and wolfSSL’s proven expertise in providing cutting-edge cryptographic solutions.
IronVelo’s Innovative Approach: The wolf-crypto Wrapper
IronVelo has developed a unique approach to integrating cryptography into their systems with their creation of “wolf-crypto.” This thin, low- to zero-cost wrapper around wolfSSL’s wolfCrypt library is designed to enforce correctness, security, and standards compliance at the Rust type system level.
Instead of relying on traditional runtime checks within the C layer, wolf-crypto elevates most constraints to compile time. This innovative strategy prevents cryptographic misuse from even compiling, enabling the early detection of bugs and the complete avoidance of undefined behavior. IronVelo has applied this rigorous methodology to FIPS-compliant usage, incorporating enforcement through both a feature flag and a marker trait to simplify compliance.
Rigorous Testing for Unwavering Reliability
IronVelo’s commitment to security extends to their thorough testing practices. To ensure compatibility with the underlying wolfCrypt implementation, they employ rigorous validation against the NIST CAVP test suite. This is further supplemented by extensive property-based testing, fuzzing, and unit tests designed to uncover edge cases. Additionally, wolf-crypto provides useful constant-time utilities that are formally verified with CBMC and Haybale Pitchfork (UCSD’s Boolector-based SMT framework) to guarantee the absence of timing side channels.
wolfSSL: A Foundation of Performance and Security
IronVelo’s decision to partner with wolfSSL was driven by several key factors. wolfSSL’s wolfCrypt library offers the performance, certifications, and proven reliability essential for securing IronVelo’s identity provider. Resource-constrained efficiency also played a critical role—wolfSSL’s minimal footprint and high efficiency are paramount for operating in deeply constrained environments. By utilizing wolfSSL, IronVelo can confidently provide its users with a secure and dependable identity management solution.
Looking Ahead: A Powerful Partnership
While still in QA, IronVelo plans to integrate wolfCrypt for both one-time key operations and TLS integration within their identity provider. This partnership between wolfSSL and IronVelo demonstrates a shared vision for building secure systems from the ground up. By combining wolfSSL’s robust cryptographic capabilities with IronVelo’s innovative Rust-based approach, the future of identity management is poised to be more secure, ergonomic, and efficient.
Find out more about IronVelo via their website: https://ironvelo.com/ and their github https://github.com/IronVelo/wolf-crypto
If you have questions about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL now
wolfSSL Enhances PKCS7 Streaming Support with Indefinite Length Handling
wolfSSL has extended its PKCS7 capabilities to better handle indefinite length encodings, particularly in streaming scenarios. While basic support for indefinite length verification existed, recent updates have refined the wc_PKCS7_VerifySignedData() API to process multipart and indefinite length content more efficiently in a streaming manner.(wolfSSL)
Key Enhancements
- Streaming Verification: The wc_PKCS7_VerifySignedData() function now supports verifying PKCS7 data with indefinite lengths without requiring the entire content to be buffered in memory.
- Improved Decoding: Enhancements in decoding functions allow for better handling of BER-encoded PKCS7 structures with indefinite lengths.
Example Usage
The wolfssl-examples repository provides practical demonstrations of these enhancements. For instance, the pkcs7-stream-verify example illustrates how to verify PKCS7 signed data in a streaming context:
PKCS7 pkcs7;
byte buffer[BUFFER_SIZE];
int ret;
// Initialize PKCS7 structure
wc_PKCS7_Init(&pkcs7, NULL, INVALID_DEVID);
// Set up certificate and key
pkcs7.cert = cert;
pkcs7.certSz = certSz;
pkcs7.privateKey = key;
pkcs7.privateKeySz = keySz;
// Begin streaming verification
ret = wc_PKCS7_VerifySignedData(&pkcs7, buffer, bufferSz);
if (ret != 0) {
// Handle error
}
// Continue processing as needed
This approach allows applications to process and verify large or streaming PKCS7 data efficiently, without the need to load the entire content into memory.
Benefits
- Efficiency: Reduces memory usage by processing data in chunks.
- Flexibility: Supports a wider range of PKCS7 encoding scenarios, including those using indefinite lengths.
- Standards Compliance: Aligns with BER encoding standards for PKCS7 structures.(GitHub)
These enhancements make wolfSSL more adaptable for applications requiring secure, real-time data processing.
If you have questiona about any of the above, please contact us at facts@wolfSSL.com or call us at +1 425 245 8247.
Download wolfSSL Now
Weekly updates
Archives
- July 2025 (15)
- June 2025 (22)
- May 2025 (25)
- April 2025 (24)
- March 2025 (22)
- February 2025 (21)
- January 2025 (23)
- December 2024 (22)
- November 2024 (29)
- October 2024 (18)
- September 2024 (21)
- August 2024 (24)
- July 2024 (27)
- June 2024 (22)
- May 2024 (28)
- April 2024 (29)
- March 2024 (21)
- February 2024 (18)
- January 2024 (21)
- December 2023 (20)
- November 2023 (20)
- October 2023 (23)
- September 2023 (17)
- August 2023 (25)
- July 2023 (39)
- June 2023 (13)
- May 2023 (11)
- April 2023 (6)
- March 2023 (23)
- February 2023 (7)
- January 2023 (7)
- December 2022 (15)
- November 2022 (11)
- October 2022 (8)
- September 2022 (7)
- August 2022 (12)
- July 2022 (7)
- June 2022 (14)
- May 2022 (10)
- April 2022 (11)
- March 2022 (12)
- February 2022 (22)
- January 2022 (12)
- December 2021 (13)
- November 2021 (27)
- October 2021 (11)
- September 2021 (14)
- August 2021 (10)
- July 2021 (16)
- June 2021 (13)
- May 2021 (9)
- April 2021 (13)
- March 2021 (24)
- February 2021 (22)
- January 2021 (18)
- December 2020 (19)
- November 2020 (11)
- October 2020 (3)
- September 2020 (20)
- August 2020 (11)
- July 2020 (7)
- June 2020 (14)
- May 2020 (13)
- April 2020 (14)
- March 2020 (4)
- February 2020 (21)
- January 2020 (18)
- December 2019 (7)
- November 2019 (16)
- October 2019 (14)
- September 2019 (18)
- August 2019 (16)
- July 2019 (8)
- June 2019 (9)
- May 2019 (28)
- April 2019 (27)
- March 2019 (15)
- February 2019 (10)
- January 2019 (16)
- December 2018 (24)
- November 2018 (9)
- October 2018 (15)
- September 2018 (15)
- August 2018 (5)
- July 2018 (15)
- June 2018 (29)
- May 2018 (12)
- April 2018 (6)
- March 2018 (18)
- February 2018 (6)
- January 2018 (11)
- December 2017 (5)
- November 2017 (12)
- October 2017 (5)
- September 2017 (7)
- August 2017 (6)
- July 2017 (11)
- June 2017 (7)
- May 2017 (9)
- April 2017 (5)
- March 2017 (6)
- January 2017 (8)
- December 2016 (2)
- November 2016 (1)
- October 2016 (15)
- September 2016 (6)
- August 2016 (5)
- July 2016 (4)
- June 2016 (9)
- May 2016 (4)
- April 2016 (4)
- March 2016 (4)
- February 2016 (9)
- January 2016 (6)
- December 2015 (4)
- November 2015 (6)
- October 2015 (5)
- September 2015 (5)
- August 2015 (8)
- July 2015 (7)
- June 2015 (9)
- May 2015 (1)
- April 2015 (4)
- March 2015 (12)
- January 2015 (4)
- December 2014 (6)
- November 2014 (3)
- October 2014 (1)
- September 2014 (11)
- August 2014 (5)
- July 2014 (9)
- June 2014 (10)
- May 2014 (5)
- April 2014 (9)
- February 2014 (3)
- January 2014 (5)
- December 2013 (7)
- November 2013 (4)
- October 2013 (7)
- September 2013 (3)
- August 2013 (9)
- July 2013 (7)
- June 2013 (4)
- May 2013 (7)
- April 2013 (4)
- March 2013 (2)
- February 2013 (3)
- January 2013 (8)
- December 2012 (12)
- November 2012 (5)
- October 2012 (7)
- September 2012 (3)
- August 2012 (6)
- July 2012 (4)
- June 2012 (3)
- May 2012 (4)
- April 2012 (6)
- March 2012 (2)
- February 2012 (5)
- January 2012 (7)
- December 2011 (5)
- November 2011 (7)
- October 2011 (5)
- September 2011 (6)
- August 2011 (5)
- July 2011 (2)
- June 2011 (7)
- May 2011 (11)
- April 2011 (4)
- March 2011 (12)
- February 2011 (7)
- January 2011 (11)
- December 2010 (17)
- November 2010 (12)
- October 2010 (11)
- September 2010 (9)
- August 2010 (20)
- July 2010 (12)
- June 2010 (7)
- May 2010 (1)
- January 2010 (2)
- November 2009 (2)
- October 2009 (1)
- September 2009 (1)
- May 2009 (1)
- February 2009 (1)
- January 2009 (1)
- December 2008 (1)

